> DOWNLOAD PDF
A simplified definition of modal analysis can be made by comparing it to frequency analysis. In frequency analysis, a complex signal is resolved into a set of simple sine waves with individual frequency and amplitude parameters. In modal analysis, a complex deflection pattern (of a vibrating structure) is resolved into a set of simple mode shapes with individual frequency and damping parameters.
Experimental Modal Analysis
Most structures vibrate. In operation, all machines, vehicles, and buildings are subjected to dynamic forces that cause vibrations. Very often the vibrations have to be investigated, either because they cause an immediate problem, or because the structure has to be "cleared" to a "standard" or test specification. Whatever the reason, we need to quantify the structural response in some way, so that its implication on factors such as performance and fatigue can be evaluated.
By using signal-analysis techniques, we can measure vibration on the operating structure and make a frequency analysis. The frequency spectrum description of how the vibration level varies with frequency can then be checked against a specification. This type of testing will give results that are only relevant to the measured conditions. The result will be a product of the structural response and the spectrum of an unknown excitation force, it will give little or no information about the characteristics of the structure itself.
An FRF measurement made on any structure will show its response to be a series of peaks. The individual peaks are often sharp, with identifiable center frequencies, indicating that they are resonances, each type of the response of a single-degree-of-freedom (SDOF) structure. If the broader peaks in the FRF are analyzed with increased frequency resolution, two or more resonances are usually found close together.
The implication is that a structure behaves as if it is a set of SDOF substructures. This is the basis of modal analysis, through which the behaviour of a structure can be analyzed by identifying and evaluating all the resonances, or modes, in its response.
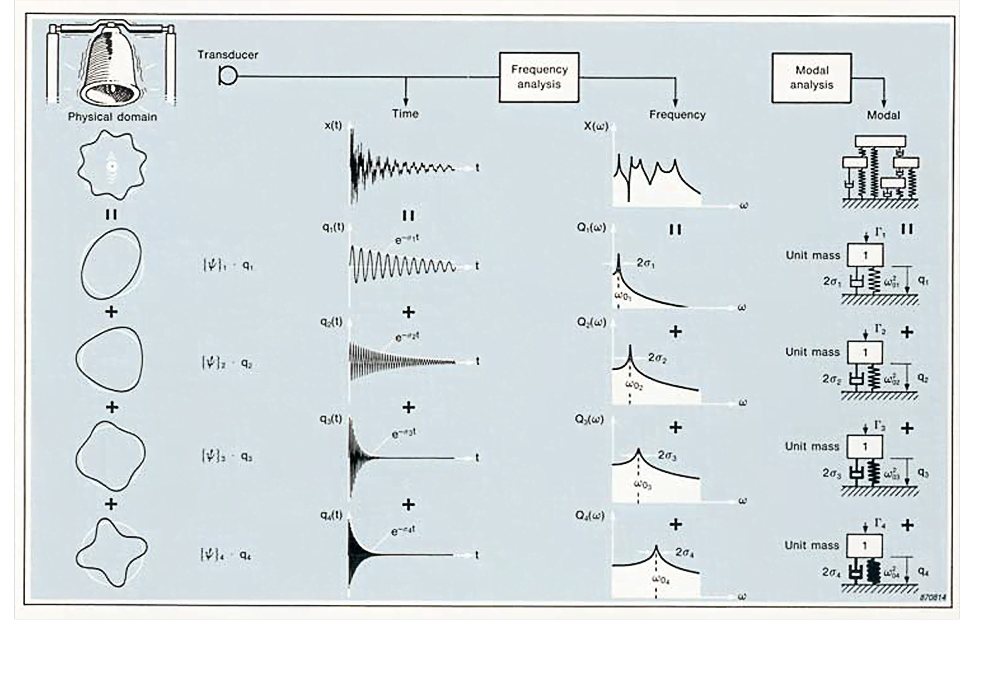
In the time domain the vibration (or acoustic) response of the bell is shown as a time history, which can be represent- ed by a set of a decaying sinusoids.
In the frequency domain, analysis of the time signal gives us a spectrum containing a series of peaks, shown below as a set of SDOF response spectra.
In the modal domain we see the response of the bell as a modal model constructed from a set of SDOF models. Since a mode shape is the pattern of movement for all the points on the structure at a modal frequency, a single mod- al coordinate q can be used to represent the entire movement contribution of each mode.
Looking back from the modal domain, we see that each SDOF model is associated with a frequency, a clamping and a mode shape.
These are the modal parameters:
- Modal frequency
- Modal damping
- Mode shape
Together the modal parameters form a complete description of the inherent dynamic characteristics of the bell, and are constant whether the bell is ringing or not. Modal analysis is the process of determining the modal parameters of a structure for all modes in the frequency range of interest. The ultimate goal is to use these parameters to construct a modal model of the response.
What is a Mode Shape?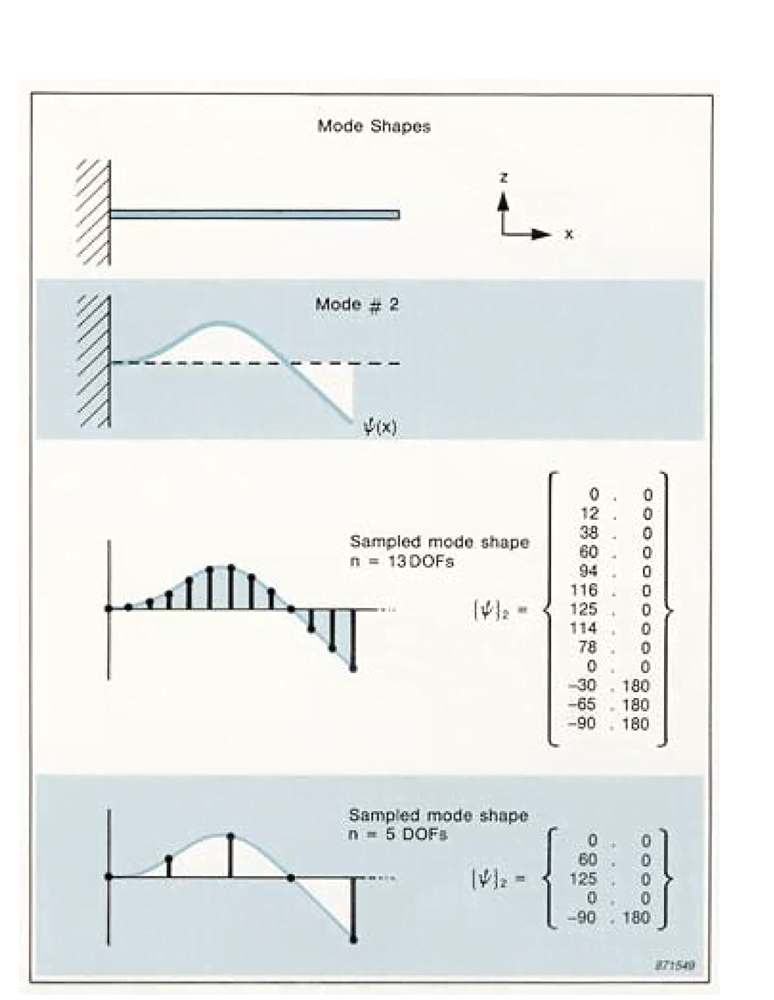
A mode shape is, as we said in the bell example, a deflection-pattern associated with a particular modal frequency - or pole location. It is neither tangible nor easy to observe. It is an abstract mathematical parameter that defines a deflection pattern as if that mode existed in isolation from all others in the structure.
The actual physical displacement, at any point, will always be a combination of all the mode shapes of the structure. With harmonic excitation close to a modal frequency, 95% of the displacement may be due to that particular mode shape, but random excitation tends to produce an arbitrary "shuffling" of contributions from all the mode shapes.
Nevertheless, a mode shape is an inherent dynamic property of a structure in "free" vibration (when no external forces are acting). It represents the relative displacements of all parts of the structure for that particular mode.
Sampled Mode Shapes: The Mode Shape Vector
Mode shapes are continuous functions that, in modal analysis, are sampled with a "spatial resolution" depending on the number of DOFs used. In general, they are not measured directly but determined from a set of FRF measurements made between the DOFs.A sampled mode shape is represented by the mode shape vector {Ψ}r, where r is the mode number.
Related Articles
Download the full handbook
Please sign in to download.
Sign-up is free and gives you full access to our Knowledge Center, with guides, primers and handbooks, technical notes and more.


