为了产生声音,必须将能量转换为机械振荡,并且这些振荡必须有效地传递到空气中。对于扬声器,其电能已经包含所需振荡序列的信号。线圈和磁铁之间的电磁相互作用将电能转换为膜的机械运动,然后将其传递到空气中。
但是,在许多系统中,所提供的能量并不具有振荡形式。对于吉他,我们通过拉弦为系统供能量。松开弦后,弦会因张力与其质量之间的相互作用而产生振动。简而言之,每当拨弦时,拉力将试图使其恢复默认位置,即两个锚点之间的直线。这会加速琴弦振动,使琴弦获得动量,使琴弦经过中间位置并偏转到另一侧。反过来,这会重新激活试图拉直琴弦的力。这种过程一次又一次地重复以产生振荡。
琴弦运动拨弦的慢动作播放显示——不是从一侧摆动到另一侧——琴弦的“三角”位移将以两个扭结为周期移动,请参见框图1。原因很简单,因为该弦是一个波导。类似于在空中传播的声波,能量以波的形式在弦上传播,从扰动的初始点传播,然后在弦的锚点之间来回移动。但是,可以从不同的角度看待振动:将其视作多个所谓驻波的组合。驻波是波峰和波谷具有固定位置的一种模式,因此与正常波运动相反,我们看不到它们行进。它们是波沿着波导以相反的方向传播并相互干扰、相互叠加或抵消的结果。
观察者将体验到这种组合的结果。如果相向行波的定时使得这些相长干涉和相消干涉总是发生在同一位置,那么就不会有传播的感觉。相反,这些波似乎停滞不前,但有一个振荡幅度。
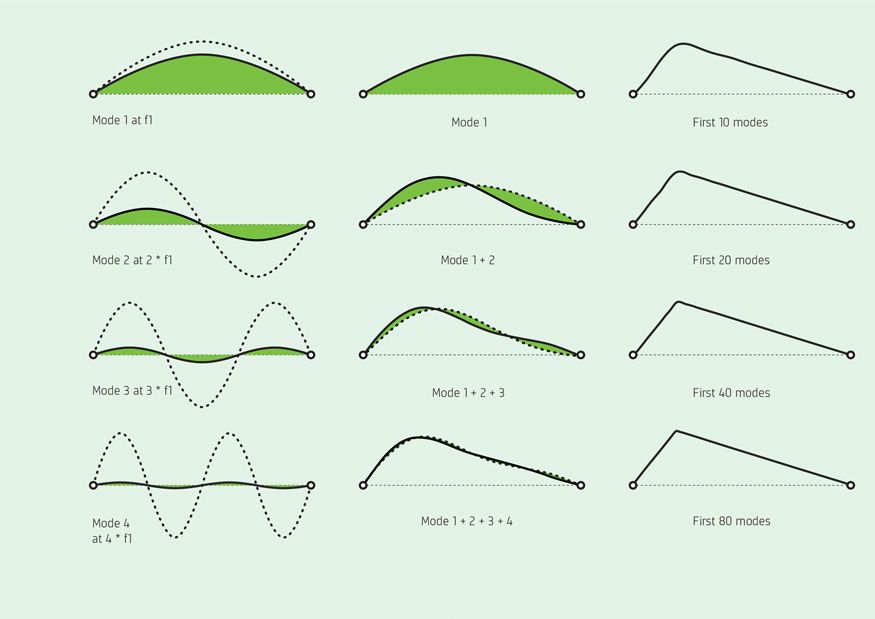
这些驻波中的每一个波都与一个频率相关,频率是指弦以该模式从一侧摆动到另一侧的每秒循环数,请参见框图2。可以在弦的固定端点之间容纳的最长波长的形状是半正弦波。其重复率最低。该频率被称为基本频率,它是我们感知为弦乐产生的音高的频率。其他模式以基本频率的几乎完美倍数重复——对于基本频率的每个周期,其他模式已经重复了两个或更多周期。波形越复杂,其关联频率越高。这些额外的频率称为泛音,它们使声音变得更丰富。
这些波形中的每一个仅从一侧移动到另一侧时,将它们的位移加在一起就会产生行进的三角形干扰。查看随时间变化的振动(行进的扭结)或考虑单个频率(驻波)就像是同一枚硬币的两个面。它们紧密相连:它们只是提供对同一过程的不同见解。