WHAT YOU WILL LEARN
- Sound Pressure And Sound Power
- What is Sound Intensity?
- Why Measure Sound Intensity?
- Sound Fields
- Pressure And Particle Velocity
GET THE FULL HANDBOOK
SOUND INTENSITY
BY BRÜEL & KJÆR
DOWNLOAD NOW
The air pressure variations that we perceive as sound can be measured simply using a sound level meter. These sound pressure level measurements provide an accurate picture of the sound levels at the measurement point, but they are not always sufficient to answer questions about the sources of that sound.
So before we understand what sound intensity is, and how to measure it, we need to understand how it relates to sound pressure and sound power.
Sound Pressure And Sound Power
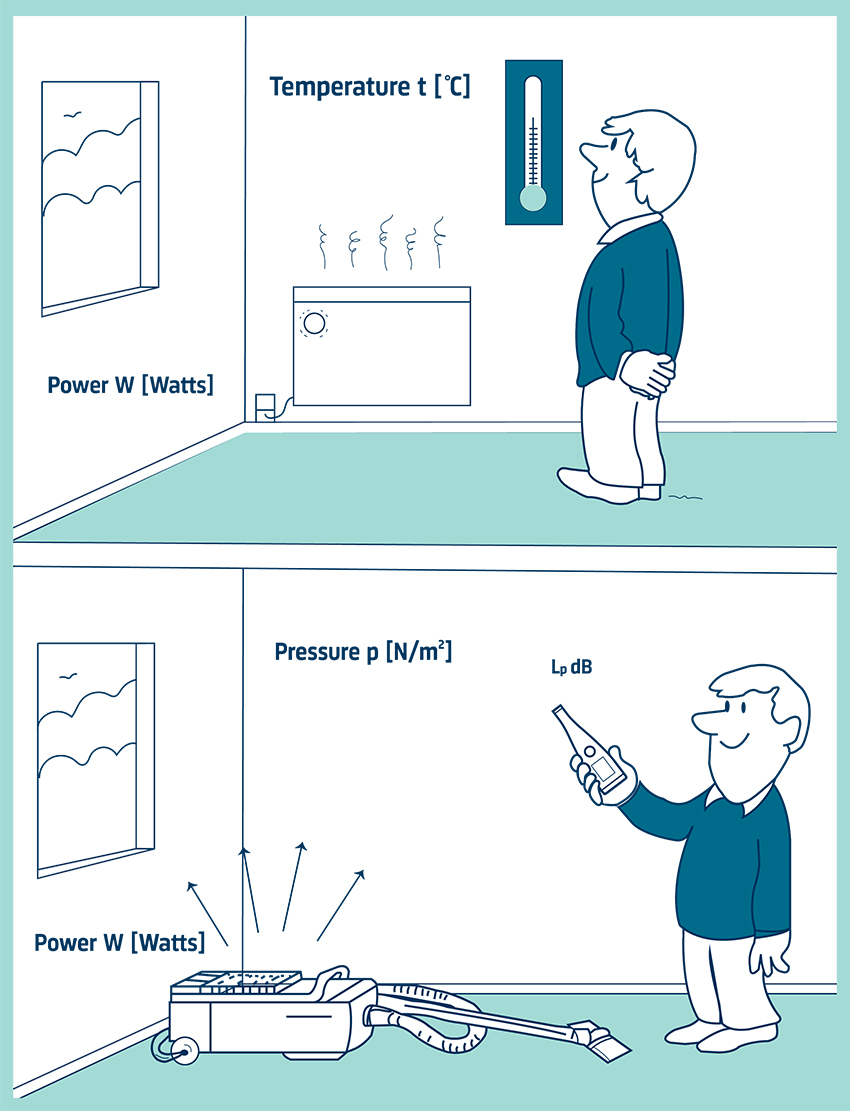
A sound source radiates power, and this results in sound pressure. Sound power is the cause. Sound pressure is the effect.
Consider the following analogy: An electric heater radiates heat into a room and temperature is the effect. Temperature is also the physical quantity that makes us feel hot or cold. The temperature in the room is obviously dependent on the room itself, the insulation, and whether other sources of heat are present. But for the same electrical power input, the heater radiates the same power, practically independent of the environment.
The relationship between sound power and sound pressure is similar. What we hear is sound pressure, but it is caused by the sound power emitted from the source.
The sound pressure that we hear or measure with a microphone is dependent on the distance from the source and the acoustic environment (or sound field) in which sound waves are present. This in turn depends on the size of the room and the sound absorption of the surfaces. So, by measuring sound pressure we cannot necessarily quantify how much noise a machine makes.
We have to find the sound power because this quantity is more or less independent of the environment and is the unique descriptor of the noisiness of a sound source.
What is Sound Intensity?
Any piece of machinery that vibrates radiates acoustical energy. Sound power is the rate at which energy is radiated (energy per unit time). Sound intensity describes the rate of energy flow through a unit area. In the SI system of units, the unit area is 1 m2. And hence the units for sound intensity are Watts per square meter.
Sound intensity also gives a measure of direction as there will be energy flow in some directions but not in others. Therefore, sound intensity is a vector quantity as it has both magnitude and direction. On the other hand, pressure is a scalar quantity as it has magnitude only. Usually, we measure the intensity in a direction normal (at 90°) to a specified unit area through which the sound energy is flowing.
We also need to state that sound intensity is the time-averaged rate of energy flow per unit area. In some cases, energy may be traveling back and forth. This will not be measured; if there is no net energy flow there will be no net intensity.
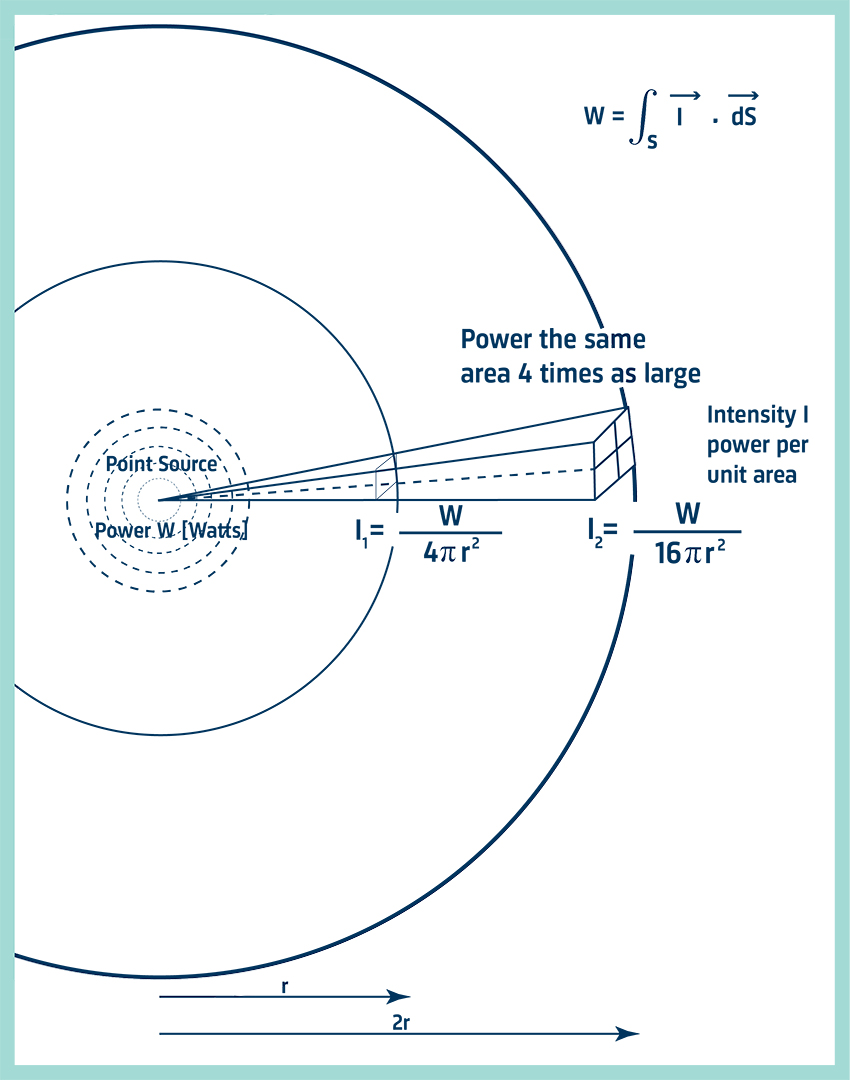
In the diagram below, the sound source is radiating energy. All this energy must pass through an area enclosing the source. Since intensity is the power per area, we can easily measure the normal spatial-averaged intensity over an area that encloses the source and then multiply it by the area to find the sound power. Note that intensity (and pressure) follows the inverse square law for free field propagation.
This can be seen in the diagram, at a distance 2r from the source the area enclosing the source is 4 times as large as the area at a distance r. Yet the power radiated must be the same whatever the distance and consequently the intensity, the power per area, must decrease.
Why Measure Sound Intensity?
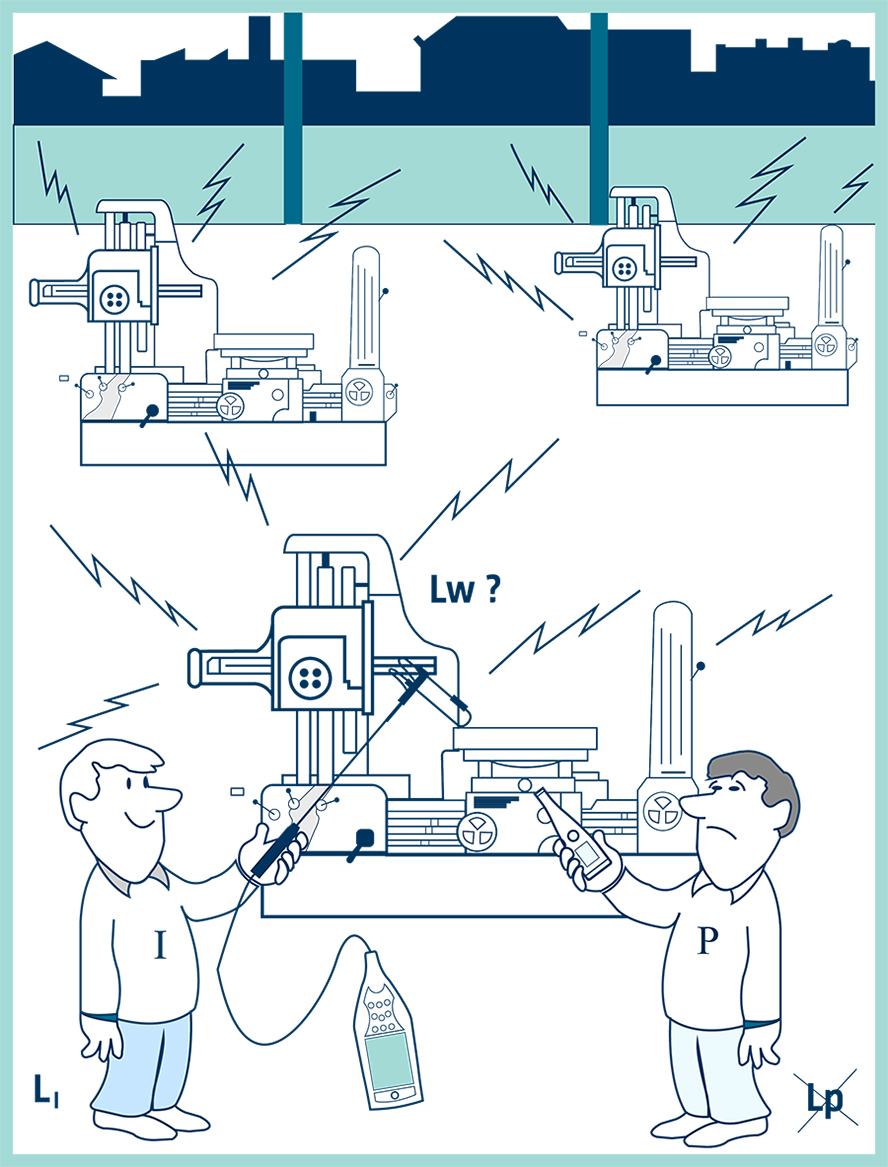
We can determine the sound power of an object from measurements of sound pressure, but there are practical challenges. While sound power can be related to sound pressure, it is only under carefully controlled conditions where special assumptions are made about the sound field. Specially constructed rooms such as anechoic or reverberant chambers fulfill these requirements. Traditionally, to measure sound power, the noise source had to be placed in these rooms.
Sound intensity, however, can be measured in any sound field. No assumptions need to be made. This property allows all the measurements to be done directly in situ. And measurements on individual machines or individual components can be made even when all the others are radiating noise because steady background noise makes no contribution to the sound power determined when measuring intensity.
Because sound intensity gives a measure of direction as well as magnitude it is also very useful when locating sources of sound. Therefore, the radiation patterns of complex vibrating machinery can be studied in situ.
Sound Fields
A sound field is a region where there is sound. It is classified according to the manner and the environment in which the sound waves travel. Some examples will now be described and the relationship between pressure and intensity discussed. This relationship is precisely known only in the first two special cases described below.
The Free Field
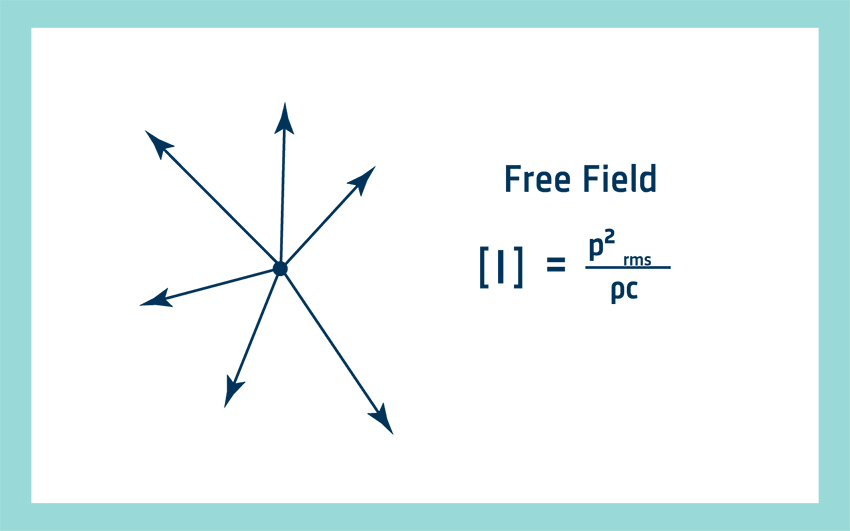
This term describes sound propagation in an idealized free space where there are no reflections. These conditions hold in the open air (sufficiently far enough away from the ground) or in an anechoic room where all the sound striking the walls is absorbed. Free field propagation is characterized by a 6 dB drop in sound pressure level and intensity level (in the direction of sound propagation) each time the distance from the source is doubled. This is simply a statement of the inverse square law. The relationship between sound pressure and sound intensity (magnitude only) is also known. It gives one way of finding sound power, which is described in the International Standards ISO 3744, 3745, and 3746.
The Diffuse Field
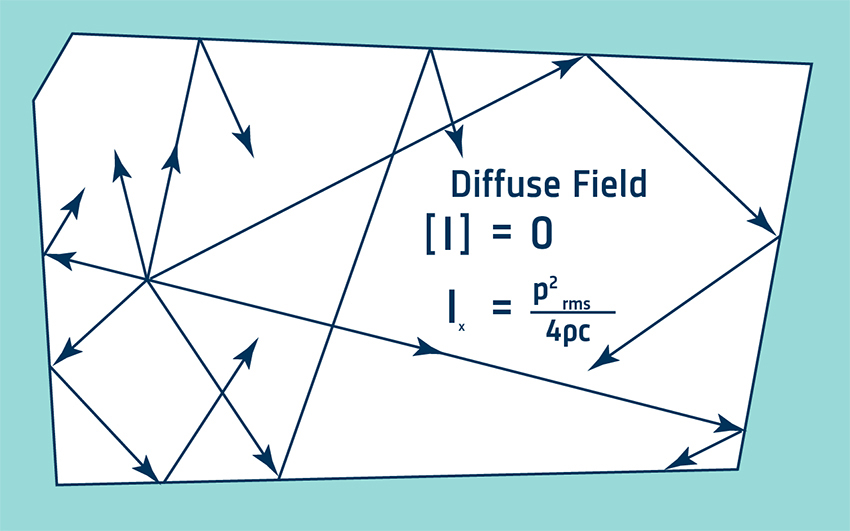
In a diffuse field, the sound is reflected so many times that it travels in all directions with equal magnitude and probability. This field is approximated in a reverberant room. Although the net intensity is zero, there is a theoretical relationship that relates the pressure in the room to the one-sided Intensity, Ix. This is the intensity in one direction, ignoring the equal and opposite component. One-sided intensity cannot be measured by a sound intensity analyzer but it is nevertheless a useful quantity: by measuring pressure, we can use the relationship between pressure and one-sided intensity to find the sound power. This is described in ISO 3741, 3743, and 3747.
Active and Reactive Sound Fields
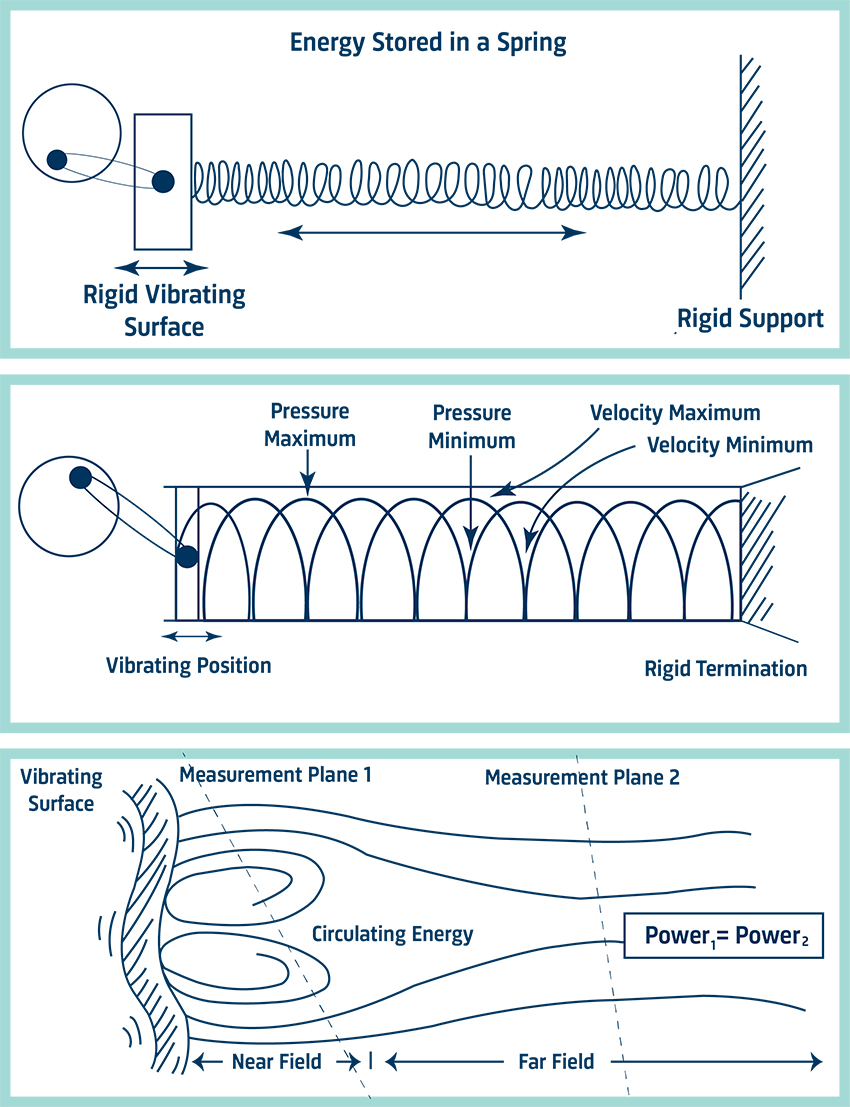
Sound propagation involves energy flow but there can still be a sound pressure even when there is no propagation. An active field is one where there is energy flow. In a pure reactive field, there is no energy flow. At any instant, energy may be traveling outward, but it will always be returned at a later instant. The energy is stored as if in a spring. Hence the net intensity is zero. In general, a sound field will have both active and reactive components. Pressure measurements for sound power in fields, which are not well-defined, can be unreliable since the reactive part is unrelated to the power radiated. We can, however, measure sound intensity. Since sound intensity describes energy flow, there will be no contribution from the reactive component of the field. Two examples of reactive fields follow.
Standing Waves in a Pipe
Consider a piston exciting the air at one end of a tube. At the other end, there is a termination which causes the sound waves to be reflected. The combination of the forward-traveling and reflected waves produces patterns of pressure maxima and minima, which occur at fixed distances along the tube. If the termination is completely rigid, all the energy is reflected and the net intensity is zero. With an absorptive termination, some intensity will be measured. Standing waves are also present in rooms at low frequencies.
The Near Field of a Source
Very close to a source, the air acts as a mass-spring system that stores the energy. The energy circulates without propagating and the region in which it circulates is called the near field. Only sound intensity measurements for sound power determination can be made here. And because it is possible to get close to the source, the signal-to-noise ratio is improved.
Pressure and Particle Velocity
When a particle of air is displaced from its mean position, there is a temporary increase in pressure. The pressure increase acts in two ways: to restore the particle to its original position, and to pass on the disturbance to the next particle. The cycle of pressure increases (compressions) and decreases (rarefactions) propagates through the medium as a sound wave.
There are two important parameters in this process: 
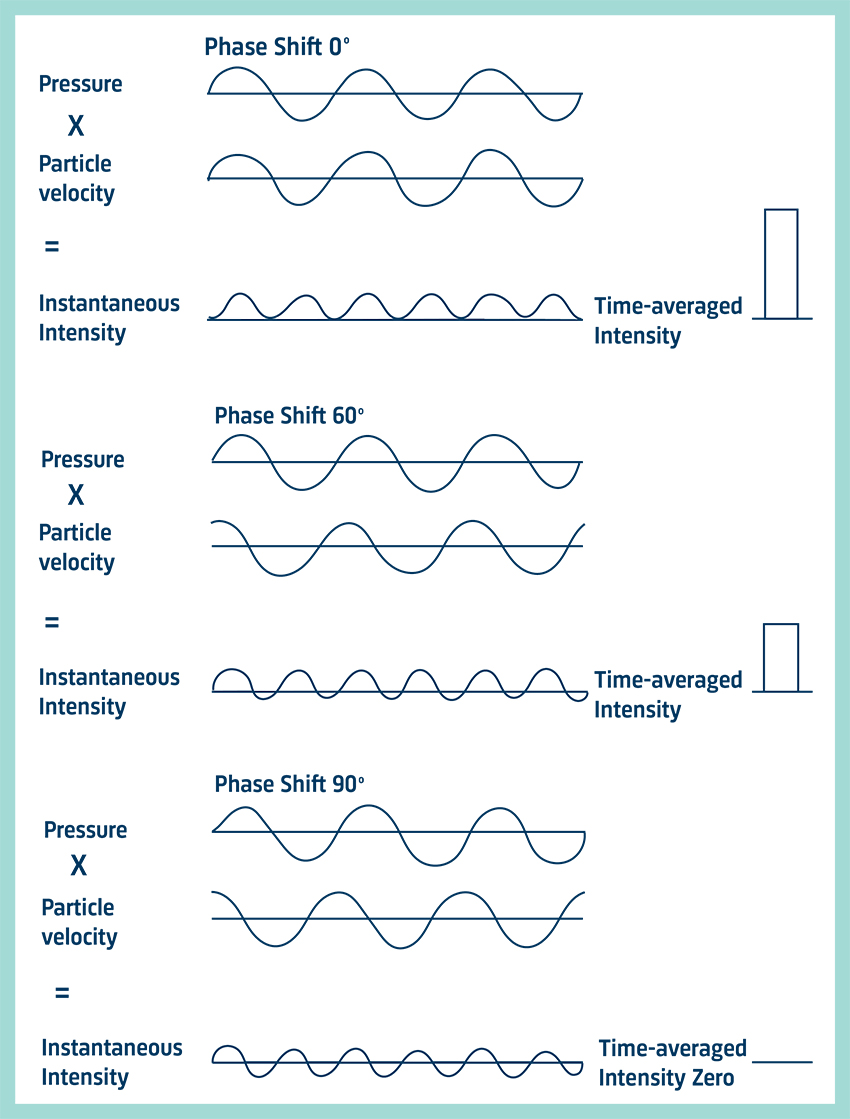
In an active field, pressure and particle velocity vary simultaneously. A peak in the pressure signal occurs at the same time as a peak in the particle velocity signal. They are, therefore, said to be in phase and the product of the two signals gives a net intensity. In a reactive field, the pressure and particle velocity are 90° out of phase. One is shifted a quarter of a wavelength with respect to the other. Multiplying the two signals together gives an instantaneous intensity signal varying sinusoidally about zero. Therefore, the time-averaged intensity is zero. In a diffuse field, the pressure and particle velocity phase vary at random and so the net intensity is zero.
Download the full handbook
Please sign in or create a profile to download.
Creating a profile is free and provides you full access to our Knowledge Center containing guides, primers and handbooks and technical reviews.