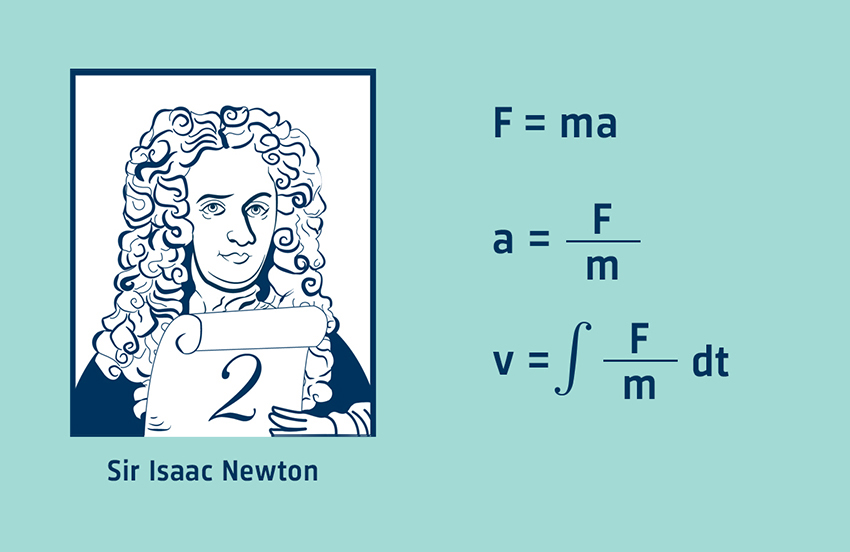音響インテンシティ
ブリュエル・ケアー
ダウンロードはこちら
音響インテンシティの測定方法
オイラー方程式
音響インテンシティは、音圧と粒子速度を時間平均した積です。音圧は1本のマイクロホンで測定できるので問題ありませんが、粒子速度の測定はそれほど簡単ではありません。しかし粒子速度は、圧力勾配(ある瞬間における圧力の距離による変化の割合)と線形オイラー方程式から導き出すことができます。近接する2つのマイクロホンでこの圧力勾配を測定し、そこから粒子速度を算出するのです。
オイラー方程式は、基本的にはニュートンの第二法則を流体に適用したものです。ニュートンの第二法則は、質量に与えられる加速度と、その質量に作用する力の関係です。力と質量がわかっていれば加速度が求まり、それを時間積分することで速度を求めることができます。
学習内容
オイラー方程式において、密度ρの流体を加速させるのは圧力勾配です。圧力勾配と流体の密度から、粒子の加速度を計算することができます。この加速度を積分すると、粒子速度が得られるのです。
有限差分近似法
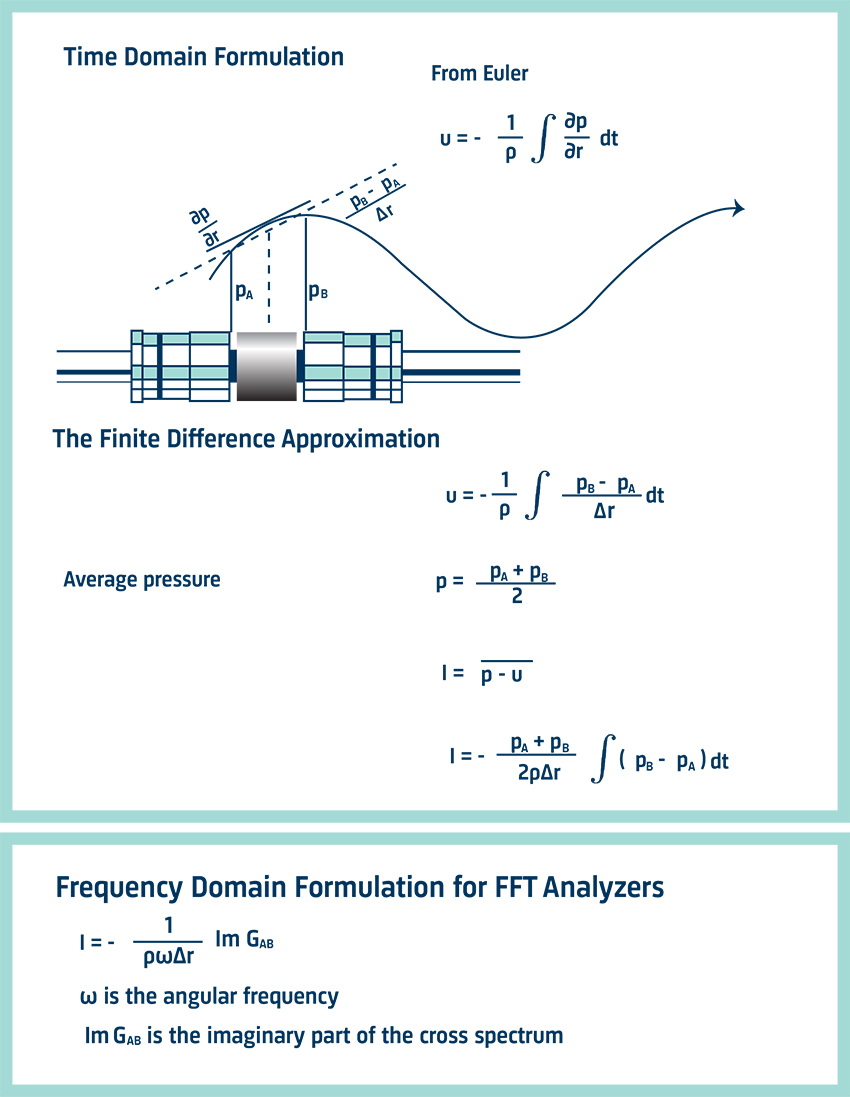
圧力勾配は連続関数であり、滑らかに変化する曲線です。近接する2つのマイクロホンの音圧差を取り、マイクロホン間の距離で割ることで、圧力勾配の直線近似式を得ることができます。これを有限差分近似といいます。円周上の2点間に直線を引くことで、円の接線を描こうとしているようなものです。
インテンシティの計算
粒子速度を求めるためには、圧力勾配成分を積分する必要があります。粒子速度の推定は、プローブの音響中心である2つのマイクロホンの中間位置で行われます。この点での音圧は、2つのマイクロホンの平均音圧で近似されます。その後、音圧と粒子速度の信号を掛け合わせ、時間平均をとることでインテンシティを求めます。
音響インテンシティ分析システムは、プローブと分析器で構成されています。プローブは、単純に2つのマイクロホンの音圧を測定します。分析器は、音響インテンシティを求めるために必要な積分や計算を行います。
音響インテンシティプローブ
ブリュエル・ケアーのプローブは、2つのマイクロホンの間にスペーサと呼ばれる部品を挟んで向かい合わせに設置しています。この配置は、スペーサのないside-by-side、back-to-back、face-to-faceの配置に比べて周波数応答や指向特性が優れていることがわかっています。スペーサの長さは6、12、50mmの3種類あり、これでマイクロホンの距離を一定に保ちます。スペーサは、カバーする周波数範囲によって選択します。
指向特性
音響インテンシティ分析システムの指向特性は、平面的には8の字型に見えますが、これはコサイン特性と呼ばれるものです。この特性は、プローブと分析器の計算に起因します。
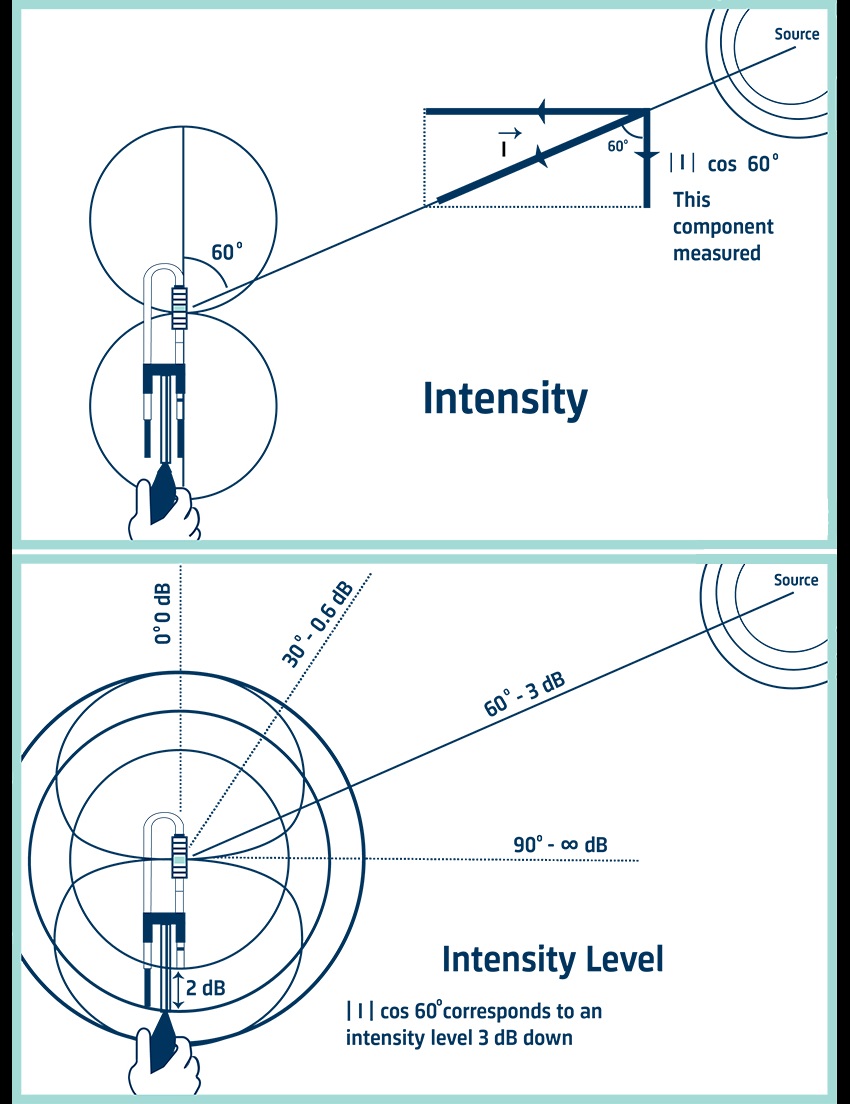
音圧はスカラー量なので、音圧測定用トランスデューサは音の入射方向に関係なく、同じ応答をする(無指向性である)必要があります。一方、音響インテンシティはベクトル量です。2本のマイクを使ったプローブでは、ベクトルを測定するのではなく、プローブの軸に沿った一方向の成分を測定します。完全なベクトルは、各座標方向に1つずつ、互いに直角な(互いに90°の)3つの成分で構成されています。
軸に対して90°の角度で入射した音は、音圧信号に差がないため、プローブの軸に沿った成分はありません。したがって、粒子速度はゼロ、インテンシティもゼロとなります。軸に対して任意の角度θで入射した音の場合、軸に沿ったインテンシティ成分は係数cosθで減少します。この減少により、指向性がコサイン特性となります。
音響インテンシティ法音響パワー
音圧ではなく音響インテンシティを用いて音響パワーを測定すると、定常的な背景騒音のある現場や機械の近傍での測定が可能となります。手法はこの上なくシンプルです。音響パワーは、音源を囲む測定面上のノーマル平均インテンシティに表面積を乗じたものです。まず、この仮想的な測定面を定義する必要があります。
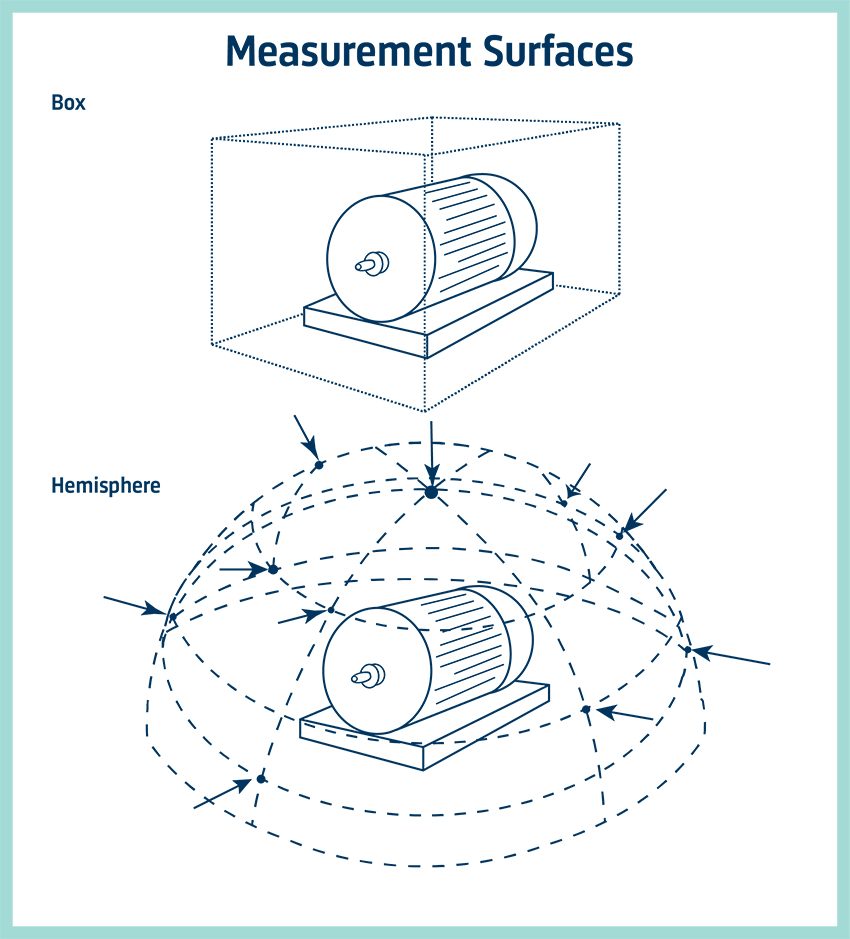
定義した測定面の内側に、他の音源や吸音材が存在しなければ、どのような形でも構いません。床はすべての音を反射すると仮定しているので、測定面には含めません。測定面は理論上、音源からの距離を問いません。以下に2つの例を示します。
直方体: どんな形や大きさでも構いません。定義しやすく、平面であることから、面上のインテンシティの平均化も簡単です。各面から部分音響パワーを求めて加算します。
半球:測定点の数を最も少なくすることができます。自由音場で無指向性音源の場合、インテンシティは半球上どこでも一様になります。
空間平均
測定面が定義されたら、測定面に対して法線方向のインテンシティを測定して空間平均する必要があります。測定面は、物理的なグリッドで定義することも、単に基準点からの距離で定義することもできます。ISO 9614には3つのパートがあり、それぞれが異なる測定方法を定義しています。パート1は離散点での平均、パート2とパート3では、測定面を掃引する(スキャニングする)平均です。パート3では、測定環境における追加の要求事項があります。
離散的な測定点で平均する方法(離散点法)
この方法では、測定面を小さなセグメントに分割し、セグメントごとに1つのポイントで個々の測定を行います。測定点は多くの場合、格子状に定義されます。定規や巻尺を使用することもできますが、フレームに糸やワイヤーを使ってガイドを作るとよいでしょう。測定結果を平均し、面積を掛け合わせると、一面の音響パワーが得られます。
どちらの方法もすべての用途に最適というわけではなく、場合によっては両方の方法が有効なこともあります。掃引法は、連続的な空間積分としてよりよい近似と言えるため、しばしばより正確な結果が得られます。ただし、プローブを一定の速度で掃引し、測定面を均等に覆うように注意する必要があります。一方、離散点法は再現性に優れています。繰り返し測定する必要がある場合は、どちらも簡単に自動化できます。これも精度の向上につながります。
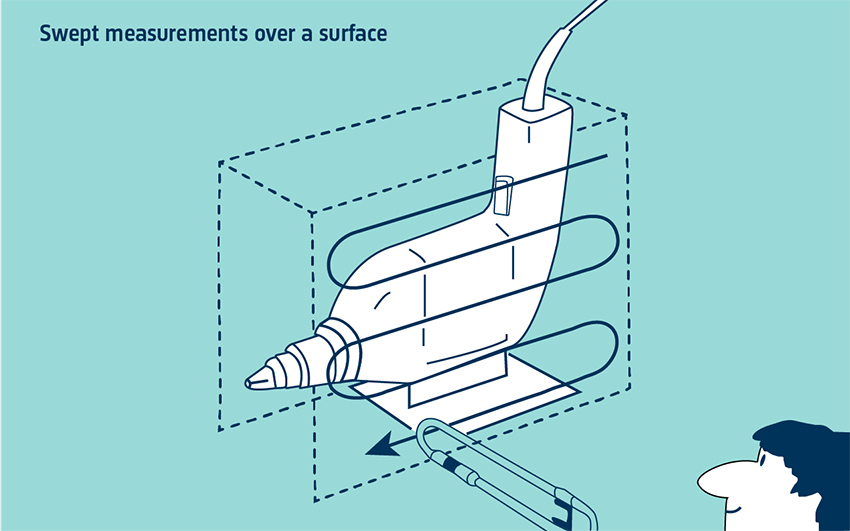
測定面を掃引する方法(スキャニング法)
適当な長さの平均化時間で、表面を塗装するような感じで、プローブで測定面上を掃引します。これにより、単一の値の空間平均インテンシティが得られます。これに面積を掛けると、この測定面からの音響パワーが得られます。そして、すべての測定面の音響パワーを合算します。