HANDBOOK | BRÜEL & KJÆR
RELEASE YEAR: 1987
DOWNLOAD FULL PDF
There are two basic types of filter used for the frequency analysis of vibration signals. The constant bandwidth type filter, where the filter is a constant absolute bandwidth, for example 3 Hz, 10 Hz etc. and the constant percentage bandwidth filter where the filter bandwidth is a constant percentage of the tuned centre frequency, for example, 3%, 10%, etc.
Frequency Scales: Linear and Logarithmic
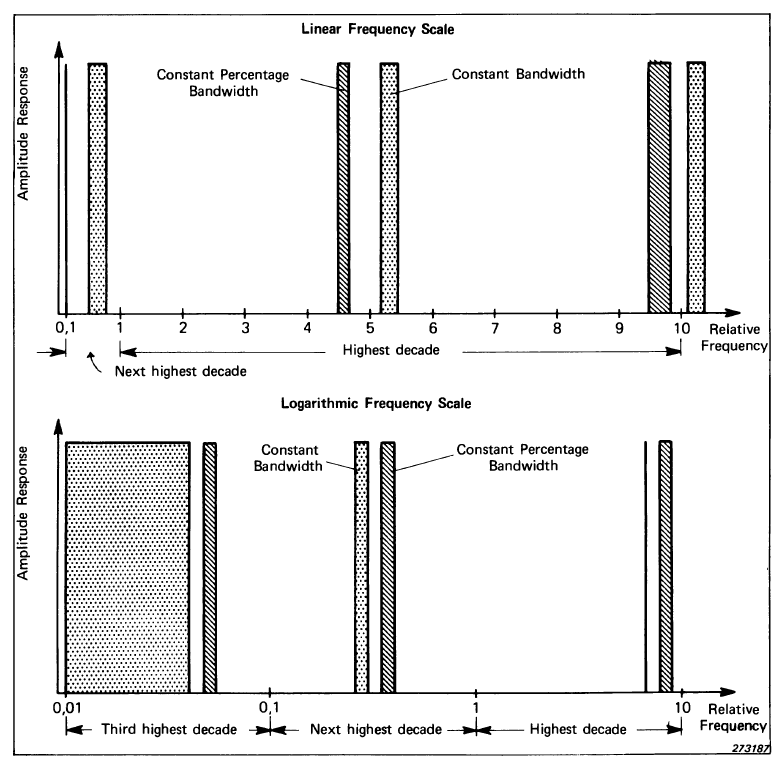
A basic choice to be made is between constant absolute bandwidth and constant relative (percentage) bandwidth where the absolute bandwidth is a fixed percentage of the tuned centre frequency. The figure below compares these two alternatives on both linear and logarithmic frequency scales and illustrates one of the most fundamental differences between them.
Constant bandwidth gives uniform resolution on a linear frequency scale and this, for example, gives equal resolution and separation of harmonically related components and this will facilitate detection of a harmonic pattern.
However, the linear frequency scale automatically gives a restriction of the useful frequency range to (at the most) two decades.
Constant percentage bandwidth, on the other hand, gives uniform resolution on a logarithmic frequency scale and thus can be used over a wide frequency range of 3 or more decades. Another feature of constant percentage bandwidth is that it corresponds to constant Q-factor (amplification ratio of resonance peaks). It is thus both natural and efficient to analyze spectra dominated by structural resonances on a logarithmic frequency scale with a constant percentage bandwidth somewhat narrower than the narrowest resonant peak.
Other grounds for using a logarithmic frequency scale (though not necessarily constant percentage bandwidth) are:
a) Small speed changes in, say, a machine only give a lateral displacement of the spectrum, thus simplifying direct comparison.
b) Certain relationships can most easily be seen on log-log scales such as, for example, integration, which gives a change in slope of –20 dB/decade and thus means that constant velocities and displacements are represented by straight lines on an acceleration vs. frequency diagram.
It is worth paying particular attention to two special classes of constant percentage bandwidth filters, that is, octave and third octave filters since these are widely used, in particular, for acoustic measurements.
Download the full handbook
Please sign in to get access.
Sign-up is free and gives you full access to our Knowledge Center, with guides, primers and handbooks, technical notes and more.